Experts are tested by Chegg as specialists in their subject area We review their content and useCalculate the iterated integral 2 0 1 0 (x y)2 dx dy Expert Answer Who are the experts? If y = \(\sqrt{\frac{sec\,x1}{sec\,x1}}\) then dy/dx = ?
Www3 Nd Edu
(x+1)dy/dx-y=e^3x(x+1)^2
(x+1)dy/dx-y=e^3x(x+1)^2-See the answer See the answer See the answer done loading Calculate the iterated integral 4 1 2 x y y x dy dx Expert Answer Who are the experts?Popular Problems Calculus Find dy/dx 2xyy^2=1 2xy − y2 = 1 2 x y y 2 = 1 Differentiate both sides of the equation d dx (2xy−y2) = d dx (1) d d x ( 2 x y y 2) = d d x ( 1) Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of 2 x y − y 2 2 x y y 2 with respect to x x is d d x 2



What Is The Solution For Math Sqrt 1 X 2 Sqrt 1 Y 2 Dx Xy Dy 0 Math Quora
Question Calculate the iterated integral 4 1 2 x y y x dy dx This problem has been solved! The solution of the differential equation `(1y^(2)) tan^(1) x dx y(1x^(2)) dy = 0` is asked in Differential Equations by PoojaBhatt ( 994k points) class12 The order and the degree of the differential equation ` y = x (dy)/(dx) 2/(dy//dx)` are A 1,2 B 1,3 C 2,1 D 1,1
Example 9 Find the general solution of the differential equation 𝑑𝑦/𝑑𝑥= (𝑥1)/ (2−𝑦) , (𝑦≠2) 𝑑𝑦/𝑑𝑥= (𝑥 1)/ (2 − 𝑦) , (𝑦≠2) (2 − y) dy = (x 1) dx Integrating both sides ∫1 〖 (2−𝑦)𝑑𝑦=〗 ∫1 (𝑥1)𝑑𝑥 2y − 𝑦^2/2 = 𝑥^2/2 x c 〖4𝑦 − 𝑦〗^2/2 = (𝑥KEAM 11 If y= sin 2 cot 1√(1x/1x), then (dy/dx) is equal to (A) 2 sin 2x (B) sin 2x (1/2) (D) (1/2) (E) cos 2x Check AnsWeekly Subscription $249 USD per week until cancelled Monthly Subscription $799 USD per month until cancelled Holidays Promotion Annual Subscription $1999 USD for 12 months (40% off)
Homework Equations The Attempt at a Solution//wwwquoracom/Whatisthesolutionoffracdydx1x2y2 \frac {dy} {dx}=1x^2y^2, Given Here, \frac {dy} {dx} represents the derivative of y with respect to x I will solve for x and y, treating y as a function of x (essentially y=f (x)) \int \frac {dy} {dx}dx=\int 1x^2y^2dx dxdyD y d x = y x Separating the variables, the given differential equation can be written as 1 y d y = 1 x d x – – – ( i) With the separating the variable technique we must keep the terms d y and d x in the numerators with their respective functions Now integrating both sides of the equation (i), we have ∫ 1 y d y = ∫ 1 x d x



Solved X Y 1 Dx X 4y 1 Dy 0 Solve The Differential Equation Course Hero



How To Solve Dy Dx 1 Xy Y X Quora
8 marks (b) Determine the values of, A B and C for 3 2 1 y Ax B x Cx = − , if 2 dy dx = 2 2 1 d y dx = at the point 2,1 7 marks 19/ 29 If 2 2 4 3 5 8 y x xy − − =, find dy dx in terms of x and y Hence evaluate dy dx when 0 dy 2 and x = 5 marks 30 (a) Given 2 (1) x y x = and (2 dy Ax x B dx x =Find the values of ASolve the initial value problems x^2 dy/dx = 4x^2 x 2/ (x 1) (y 1), y (1) = 1 x^2 dy/dx 3xy = x^4 ln (x) 1, y (1) = 0 Solve the Equation dy/dx y/x 2 = 5 (x 2)y^1/2 Determine whether the equation is exact if it is then solve it 2/Squareroot 1 x^2 y cos (xy) dx x cos (xy) y^1/3 dy = 0 Solve the Equation dy/dx = xCalculus Find dy/dx y=1/ (x^2) y = 1 x2 y = 1 x 2 Differentiate both sides of the equation d dx (y) = d dx ( 1 x2) d d x ( y) = d d x ( 1 x 2) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps




Ipe Material Notes




Ex 9 4 16 For Xy Dy Dx X 2 Y 2 Find Solution
Let's simplify it First dy/dx = (y/x 1)/(y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc = arctan (y/x) 1/2 logTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `x(1y^2)dxy(1x^2) dy=0` 1 2y −1 ⋅ dy dx = 1 integrating ∫ 1 2y −1 dy dx dx = ∫ dx ∫ 1 2y −1 dy = ∫ dx 1 2 ln(2y − 1) = x C ln(2y −1) = 2x C 2y −1 = e2xC = Ce2x



What Is The Solution For Math Sqrt 1 X 2 Sqrt 1 Y 2 Dx Xy Dy 0 Math Quora




First Order Differential Equations Chapter 2 Ch2 2 Contents 2 1 Solution Curves Without A Solution 2 1 Solution Curves Without A Solution 2 2 Separable Ppt Download
I'm stuck on solving the following differential equation $$(x^21)(y^21)dx(x1)(y2)dy=0$$ Obviously it's not exact, because $\frac{d((x^21)(y^21))}{dy}\neq\fracCalculus Find dy/dx y^2= (x1)/ (x1) y2 = x − 1 x 1 y 2 = x 1 x 1 Differentiate both sides of the equation d dx (y2) = d dx ( x−1 x1) d d x ( y 2) = d d x ( x 1 x 1) Differentiate the left side of the equation Tap for more steps Ex 94, 12 Find a particular solution satisfying the given condition 𝑥 𝑥2−1 𝑑𝑦𝑑𝑥=1;𝑦=0 When 𝑥=2 𝑥 𝑥2−1 dy = dx dy = 𝑑𝑥𝑥(𝑥2 − 1) Integrating both sides 𝑑𝑦 = 𝑑𝑥𝑥(𝑥2 − 1) 𝑦 = 𝑑𝑥𝑥(𝑥 1)(𝑥 − 1) We can write integrand as 1𝑥(𝑥 1




Solve The Following Differential Equation X 2 1 Dy Dx 2 X Y 2 X 2 1



1
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Ex 94, 6 For each of the differential equations in Exercises 1 to 10, find the general solution 𝑑𝑦/𝑑𝑥=(1𝑥^2 )(1𝑦^2 ) 𝑑𝑦/𝑑𝑥=(1𝑥^2 )(1𝑦^2 ) dy = (1𝑥^2 )(1𝑦^2 ) dx 𝑑𝑦/(1 𝑦^2 )= (1 𝑥^2) dx Integrating both sides ∫1 𝑑𝑦/(1 𝑦^2 ) = ∫1 (1𝑥2)𝑑𝑥 tan−1 y = x 𝒙^𝟑/𝟑 C If y = (1 1/x^2)/ (1 1/x^2), then dy/dx is Sarthaks eConnect Largest Online Education Community




Ecuaciones Diferenciales Guia N 2



Solve The Differential Equation X2 1 Dy Dx 2xy 1 X2 1 Studyrankersonline
This equation is an exact differential dF (x,y) = 0 because P_y = 2y/x^2 = Q_x The solution is F (x,y) = C with F_x = P = 1 y^2/x^2 1/x^2 F_y = Q = 1 2y/x Integrating the second equation leads to F (x,y) = y (y^2)/x G (x) Using the first equation gives G' (x) = 1 1/x^2 so G (x) = x(1 X) (1 Y2) Dx (1 Y) (1 X2) Dy = 0 CBSE CBSE (Science) Class 12 Question Papers 1851 Textbook Solutions MCQ Online Tests 31 Important Solutions 4564 Question Bank Solutions Concept Notes & Videos 725 Time Tables 18 Syllabus Advertisement Remove allImplicit derivative (dy)/ (dx), (xy)^2=xy1 \square!




Solved Solve Each Differential Equation Dy Dx Xy X 2 1 Chegg Com



Use Fourth Order Runge Kutta Method To Find The Value Of Y At X 1 Given That Dy Dx Y X Y X Such That Y 0 1 Taking H 0 5
Solutionput (xy)=v then differentiate both sides with respect to 'x' we get 1dy/dx=dv/dx or, dy/dx=dv/dx—1 this value put in to equation (I), first arranging equation (I) dy/dx= (xy1) (xy—2)/ (xy2) (xy—1) or, dv/dx—1= (v1) (v—2)/ (v2) (v—1) or,dv/dx= (v^2—2vv—2)/ (v^22v—v—2) 1Find the solution of the differential equation that satisfies the given initial conditiondy/dx = y^2 1, y(1) = 0 Homework Statement rewrite the equation in the form of linear equation Then solve it (1x^2)dy/dx xy = 1/ (1x^2) the ans given is y= x/ (1x^2) C / ( sqrt rt (1x^2) ) , my ans is different , which part is wrong ?



Solve The Differential Equation Dy Dx 1 X Y2 Xy2 When Y 0 X 0 Studyrankersonline




Differential Equatio Long Answer Questions 7 M R Solye 2x Y 3 Dx 2y X 1 Dy Sol Dy 2x Y 3 Given Equation Is
The issue is that you integrated y with respect to x, and concluded that it was equal to y This is only viable if y = aex for some constant a, which we have no reason to suspect Solve y ^2x (\frac {dy} {dx})^2 = 1 using proposed change of variables Solve y2 −x(dxdy )2 = 1 using proposed change of variablesCalculus Find dy/dx y^2=1/ (1x^2) y2 = 1 1 − x2 y 2 = 1 1 x 2 Differentiate both sides of the equation d dx (y2) = d dx ( 1 1−x2) d d x ( y 2) = d d x ( 1 1 x 2) Differentiate the left side of the equation Tap for more stepsKEAM 11 If y= cot 1( tan (x/2) ), then (dy/dx) is equal to (A) (1/2) (B) 0 (x/2) (D) (1/2) (E) (x/2) Check Answer and Soluti



Solve Dy Dx Xy 1 X 2 X Y Sarthaks Econnect Largest Online Education Community




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection
(x^2 – y 2) dx (x 2 2xy) dy= 0 Exercise 25 Q1 (xy) dx x dy = 0 Q2 (xy) dx x dy = 0 Q3 x dx (y 2x) dy= 0 Q5 (y 2 yx) dx – x 2 dy = 0 Q11 In Problems 11–14 solve the given initialvalue problem xy 2 dy/dx = y 3 x 3, y(1) = 2 Chapter 3 Exercise 31 Q1 The population of a community is known to increase at a rateTo solve this, let v ( y) = 1 / x ( y) Also, don't forget to pick up both branches of the solution by noting that if y ( x) is a solution, so too is − y ( x) Update Alright, here's how to do it Let v ( y) = 1 / x ( y) Then d x d y = − 1 v ( y) 2 d v d y giving(1) 2/x 2 2/x 3 (2) 2/x 3 1/x 2 (3) 2/x 2 2/x 2 (4) none of these Solution Given y = (1 – x)/x 2 = 1/x 2 – 1/x Differentiate wrtx dy/dx = 2/x 3 – (1/x 2) =



Answered N W Solve 1 Xdy 3ydx X Y Dx 2 Bartleby




Solve X X 1 Dy Dx X 2 Y X3 2x 1 Maths Application Of Derivatives Meritnation Com
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(1x^2) dy/dxxy=1` So variable separable method is not possible Now, 𝑑𝑦/𝑑𝑥 = ((1 𝑦^2))/tan^(−1)〖𝑦 − 𝑥〗 Put F(x, y) = 𝑑𝑦/𝑑𝑥 F(x, y) = (1 𝑦^2)/(tan^(−1)𝑦−𝑥) F(𝜆x, 𝜆y) = (1 𝜆^2 𝑦^2)/(tan^(−1)𝜆𝑦−𝜆𝑥)≠ 𝜆° F(x, y) Hence, the equation is not homogenous Solve (1 – x2) (dy/dx) xy = xy2 The given differential equation is Multiplying both sides of Eq (ii) by IF and integrating, we get,



D Dx Formula




Line Drawing Version B Semiformal Methods Derivation Anthony
Experts are tested by Chegg as specialists in their subject area We review their content and use your feedback to keep the quality high 100% (87 ratings) Previous question Next question Transcript Misc 11 Find a particular solution of the differential equation ( )( )= , given that = 1 , when =0 ( = ) ( )( )= y dx y dy = dx dy x dx y dx dxView QUESTION BANK ENG MATHS Ipdf from MATH MA6151 at Rajalakshmi Engineering College QUESTION BANK PART A 1Find dy dx x if y = x 2Find , when y




Solved Solve Dy Dx 1 X Y Solve Dy Dx Y X 1 Y Solve The Chegg Com



How To Get The Special Solution Of This Differential Equation Y Xdy Dx 2 1 X 2 Dy Dx Where X 1 Y 1 Quora
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!√(sec x1/sec x1) A sec2x B 1/2 sec2 x/2 C 1/2 cosec2 x/2 D none of theseSolve the differential equation dy/dx = y/x Solve the differential equation dy/dx = y/x




Solve 1 X 2 D 2y Dx 2 X Dy Dx Y X 1 X 2 3 2 Mathematics 2 Question Answer Collection




Solved The General Solution Of Dy Dx Xy 2 X Y Is In Chegg Com
6 12 8 4 dy dx 10 x x 2 1 y 3 0 60 4 6 4 6 dy dx 1 12 x 2 y 4 2 61 3 1 3 3 dy dx from TEPSERVER 231 at University of California, San Diego M110 Module 6 Advanced Functions & Logarithms 2 Power & Exponential Functions Questionsdocx y = x 1 C/e^x dy/dx=xy not separable, not exact, so set it up for an integrating factor dy/dx y =x the IF is e^(int dx) = e^x so e^x dy/dx e^x y =xe^x or d/dx (e^x y) =xe^x so e^x y = int xe^x \ dx qquad triangle for the integration, we use IBP int u v' = uv int u' v u = x, u' = 1 v' = e^x, v = e^x implies x e^x int e^x \ dx = x e^x e^x C so going back to triangle e^x y = x e Rewriting the given diff eqn (DE) as #dy/dxy=2x#, we find that it is a linear DE of the form #dy/dxyP(x)=q(x)# To find its gen soln (GS), we need to multiply it by the integrating factor (IF) #e^(intP(x)dx# Since, #P(x)=1, intP(x)dx=int1dx=x " IF is "e^x# Multiplying the DE by IF, we get, #e^xdy/dxye^x=2xe^x#




33 X 1 Dy Dx Y Ln X Y 1 10 Ecuaciones Lineales Alexander Estrada Youtube



Solve X 1 Dy Dx Y E X X 1 2 Sarthaks Econnect Largest Online Education Community
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(1x^2)dy/dx=1y^2` dy/dx=x/y x^2y^2=1 Differentiate wrt x d/dxx^2d/dxy^2=d/dx1 We already know how to deal with the first and third terms, so lets get them out the way d/dxx^2d/dxy^2=d/dx1 2xd/dxy^2=0 For the remaining term we use the chain rule, we don't know how to differentiate y^2 wrt x but we do know how to differentiate y^2 wrt y (it the same as differentiating x^2 wrt x!)Calculus Find dy/dx y=1/x y = 1 x y = 1 x Differentiate both sides of the equation d dx (y) = d dx ( 1 x) d d x ( y) = d d x ( 1 x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps



Find The General Solution Of Differential Equation X 2 Y 1 Dx Y 2 X 1 Dy 0 Sarthaks Econnect Largest Online Education Community



0以上 Y 2 Xy 1 X X 3 Y 2xy 1 Dx X 1 2xy X 3y 3 Dy 0 Saesipapictdxe
Bernoulli's equation has form, \frac{dy}{dx}p(x)y=q(x)y^n Now, consider this, \frac{dz}{dx}z^2x=z^2z This easily simplifies to, \frac{dz}{dx}z=(1x^2)z^2 where p(x)=1 Find bounded solutions of this ODE https//mathstackexchangecom/questions//findboundedsolutionsofthisode Hint on the first question f(x) = \frac{\sinh(x)}{x} =




Example 9 Find General Solution Of Dy Dx X 1 2 Y Examples




11 Xy 2 Dy Dx Y 3 X 3 Y 1 2 Soluciones Por Sustitucion Alexander Estrada Youtube



Secure Media Collegeboard Org




Solved Solve The Initial Value Problems A X 2 Dy Dx 4x 2 Chegg Com



How To Solve The Differential Equation Dy Dx Y 1 X X 1 2 1 X 1 2 Quora



Secure Media Collegeboard Org




If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib




Ex 9 4 6 Find General Solution Dy Dx 1 X2 1 Y2




Solve 1 X Dydx Xy 1 X




How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic




Math 432 Hw 2 5 Solutions




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com




The Solution Of Dy Dx X 2 Y 2 1 2xy Satisfying Y 1 0 Is Given By




Ecuaciones Diferenciales Aplicaciones



Dy Dx X 1 2 Youtube



1



Find The General Solution Of Differential Equation 1 X 2 1 Y Dx Xy 1 Y Dy Sarthaks Econnect Largest Online Education Community




Solve X X 1 Dy Dx Y X2 X 1 2 Maths Differential Equations Meritnation Com




Unit 03 Differential Equations Pdf Logical Truth Equations




Capitulo 2 Metodos De Solucion Pdf Descargar Libre




Misc 14 Find Particular Solution X 1 Dy Dx 2e Y 1




Solve The Differential Equation 1 X 2 1 Y Dx Xy 1 Y Dy Brainly In




Solucionario Ecuaciones1



Integrating Factor Of The Differential Equation 1 X2 Dy Dx Xy 1 Is Studyrankersonline




If Y X Is The Solution Of Dy Dx X 2 1 Y 2 Y 0 2 Then Y 3 Homeworklib




Engineering Mathematics Notes




Solved Solve The Following Differential Equations Question Chegg Com




Ecuaciones Diferenciales Docsity



Solved Find The Particular Solution Indicated For The Following Course Hero




Solucionario Ecuaciones1



Solve The Linear Differential Equation X 2 1 Dy Dx Xy X Youtube



Cdigital Dgb Uanl Mx




Engineering Mathematics Notes




If X 1 Y Y 1 X 0 Then Prove That 1 X 2 Dydx 1 0




Y 1 Y 2 Y 3 Royaltechsystems Co In



Solved Solve The Following Bernoulli Equations B 2 X 2 Dy Dx Xy X 3 Y 3 C Y X Y X2 5 X 2 Y 1 2 D X Dy Dx 6y 3xy Course Hero



1 X 2 Dy Dx Xy 1 1 X 2 Physics Forums



Answered 3 Y 2 Dx X Y 1 Dy 0 Bartleby




Solucionario Ecuaciones1




Doc Iii Exact Differentia Equation Joshua Pascual Academia Edu




Example 10 Find General Solution Dy Dx 1 Y2 1 X2 Examples




15 The Differential Equation 2xy Dy X2 Y2 1 Dx Determines A A Family Of Circles With Centre On X Axis B A Family Of Circles With Centre On Y Axis




If Log 1 X 2 X Y 1 X




Solved Solve The Differential Equation Dy Dx Xy 2 1 Chegg Com




Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange




Math 432 Hw 2 5 Solutions Pdf Free Download




Banco Primer Departamental De Ecuaciones Diferenciales




Find The General Solution Of The Given Differential Equation X 1 Dy Dx X 2 Y 2xe X




Solution Solve The Differential Equation X Y 1 Dx X 1 Dy 0 If Y 2 When X 1



Www3 Nd Edu




Find A Particular Solution Of The Differential Equation X 1 Dy Dx 2e Y 1 Given That Y 0 When X 0 Mathematics Shaalaa Com



Solve 1 X 2 Dy Dx Xy Xy 2 Sarthaks Econnect Largest Online Education Community



What Is The Solution Of This Differential Equation Y X 2 Y 2 1 Dx X X 2 Y 2 1 Dy 0 Quora




Ejercicios Examen Calculo Integral Y Aproximado Soluciones De Los Controles De Metodos Matematicos Studocu




Solve The Differential Equation X 1 Dydx 2x 3y



How To Find Dy Dx Of The Function Y X 1 X 2 X 1 2 Quora




1 X 2 Dy Dx Xy 1 Youtube




Wa0002 Pdf Ajedrez Juegos Y Actividades



Cdigital Dgb Uanl Mx
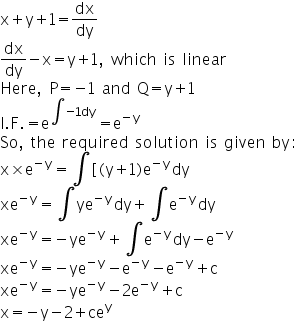



X Y 1 Dy Dx 1 Mathematics Topperlearning Com H5lpj6ff




Solve The Linear Differential Equation 1 X Dy Dx Xy 1 X Brainly In




Solucionario Ecuaciones1




Solve X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 Given That Y E X Is An Integral Included In The Complementary Function सम करण X D 2 Dx 2 2x 1 Dy Dx X 1 Y 0 क हल क ज ए द य गय ह क Y E X



1




Part A Keep In Mind That Dy Dx Is The Slope We Simply Need To Substitute X And Y Into The Differential Equation And Represent Each Answer As A Slope Ppt Download
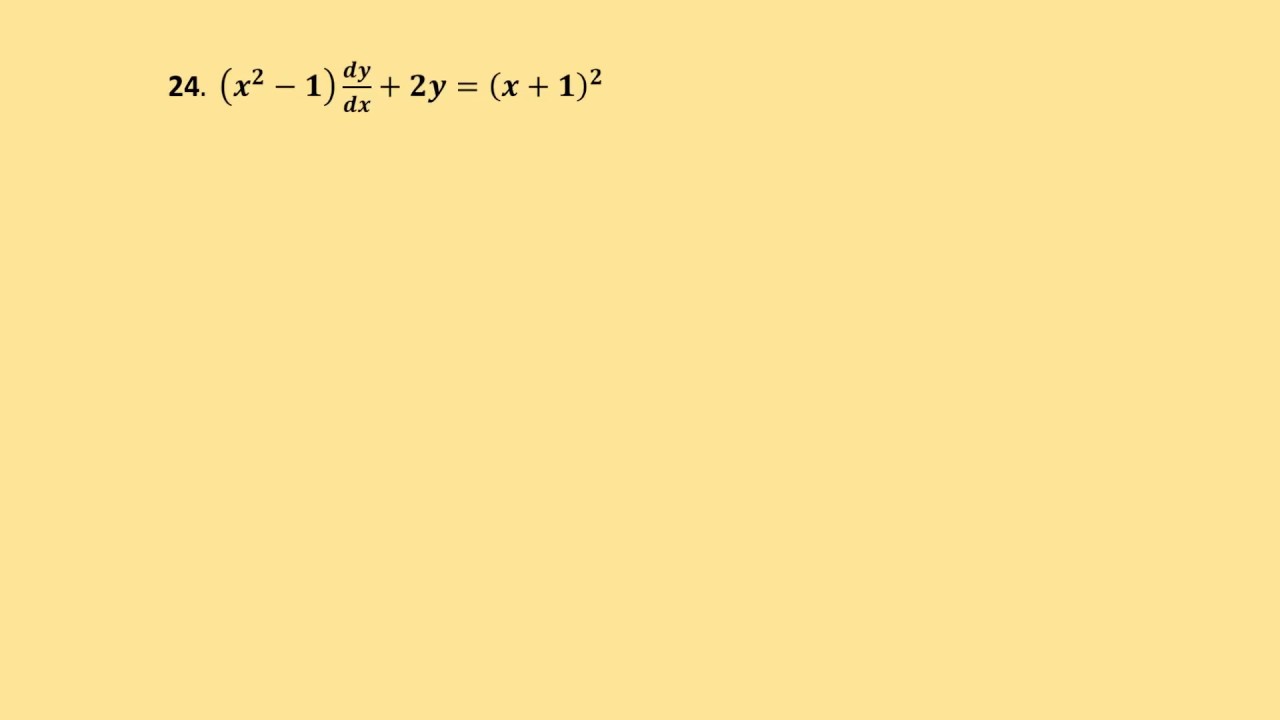



24 X 2 1 Dy Dx 2y X 1 2 Ecuaciones Lineales Youtube




Find Y X If It Satisfies The Following Differential Equation Dy Dx X Y 2 And Given That Y 1 1 A Ln 1 X Y 1 X Y 2 X 1 B Ln 2 Y 2 X X Y 1 C Ln 1 X Y 1 X Y 2 X 1 D 1 2ln 1 X Y 1 X Y Ln X 0




Find The Particular Solution Of The Differential Equation X Y Dy Dx X 2y Given That Y 0 When X 1 Mathematics Shaalaa Com




Dy Dx 1 X Y 2 Xy 2 Ecuacion Diferencial De Variables Separables Con Solucion Explicita Youtube
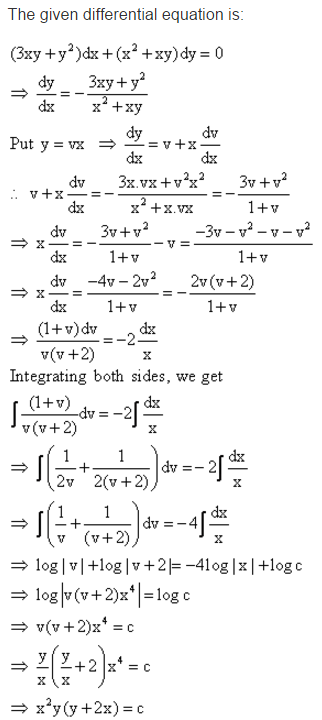



Find The Particular Solution Of Given Differential Equation 3xy Y 2 Dx X 2 Xy Dy 0 At X 1 Y 1 Mathematics Topperlearning Com D1ksg633




Solved Dy Sec Y 11 12 Du 1 4v2 Dx 1 X2 Dx 3v 13 X X X Dy Dt 14 Dx 3x 1 Y2 3 2 15 Y 1 Dy Yecos




Misc 11 Find Particular Solution X Y Dx Dy Dx Dy
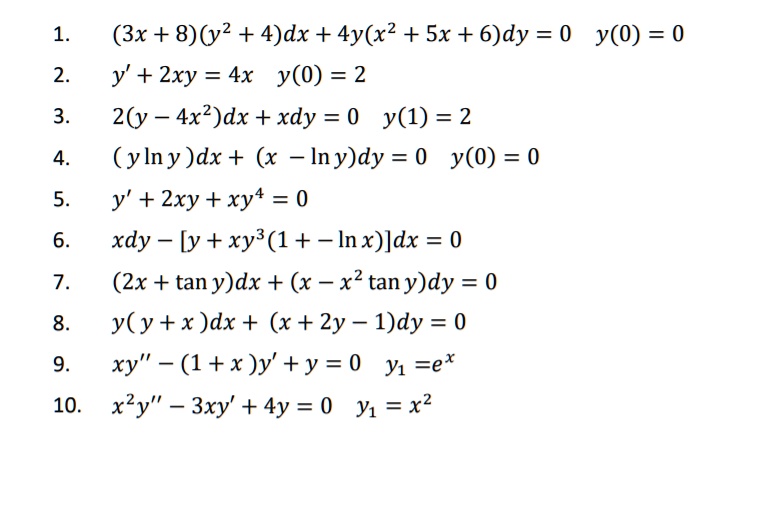



3x 8 Y2 4 Dx 4y X2 Sx 6 Dy 0 Y 0 0 Y Itprospt




Ex 9 4 12 Find Particular Solution X X2 1 Dy Dx 1 Y 0




Oneclass A Variable Separable Equations Xy X Dx X2y2 X2 Y2 1 Dy Select One A 21n X2 1




0以上 Y 2 Xy 1 X X 3 Y 2xy 1 Dx X 1 2xy X 3y 3 Dy 0 Saesipapictdxe



0 件のコメント:
コメントを投稿